1Answer
Pythagoras Theorem (पाइथागोरस प्रमेय) - परिभाषा, सूत्र और उदाहरण
पाइथागोरस प्रमेय की परिभाषा (definition of pythagoras theorem)
Pythagoras Theorem (पाइथागोरस प्रमेय)
गणित में पाइथागोरस प्रमेय बहुत ही सामान्य और महत्वपूर्ण विषय. यह समकोण त्रिभुज के विभिन्न पक्षों के बीच के संबंध की व्याख्या करता है. प्रमेय बताता है कि "एक समकोण त्रिभुज में, कर्ण का वर्ग त्रिभुज के अन्य दो पक्षों के वर्गों के योग के बराबर होता है."
अन्य दो पक्ष यहाँ त्रिभुज के लंबवत और आधार हैं। इसलिए, एक समकोण त्रिभुज में, Hypotenuse इसका सबसे लंबा भाग बन जाता है, क्योंकि यह 90 ° कोण के सामने हैं.
PYTHAGOREAN THEOREM का FORMULA
एक समकोण त्रिभुज में,
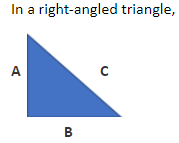
A, लंबवत है
B आधार है
C कर्ण है
Therefore, according to the definition of the Pythagorean Theorem, the formula would be:
Hypotenuse²= Perpendicular² Base²
In other words, it would be:
C²= A² B²
पाइथागोरस प्रमेय का PROOF :
समकोण त्रिभुज में, आधार और लम्ब एक-दूसरे के साथ 90 डिग्री का कोण बनाते हैं. इसलिए, पाइथागोरस प्रमेय के अनुसार, "कर्ण का वर्ग आधार के वर्ग और लंब के वर्ग के योग के बराबर है।"
“the square of the hypotenuse is equal to the sum of a base square and perpendicular square.”
“the square of the hypotenuse is equal to the sum of a base square and perpendicular square.”
इस प्रमेय को सिद्ध करने के लिए,
मान लें कि एक त्रिभुज ABC है, जिसका कोण B समकोण है.
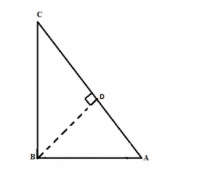
हमें सिद्ध करना है : AC²= AB² BC²
To explain: हम एक सीधा रेखा BD खींचते हैं जो D पर AC से मिलती है.
Proof:
हम प्रमेय द्वारा जानते हैं कि यदि एक समकोण त्रिभुज के कर्ण से समकोण की ओर से खींचा जाता है, तो लम्बवत् के दोनों किनारों पर दो त्रिभुज एक दूसरे के समान होते हैं.
इसलिए,
△ADB ~ △ABC
Hence,
AD/AB = AB/AC (Condition for similarity)
Or, AB2 = AD × AC (1)
Also, △BDC ~△ABC (By applying the same theorem)
Therefore,
CD/BC = BC/AC (Condition for similarity)
Or,
BC2= CD × AC (2)
Now,
By adding the equations (1) and (2) we get,
AB2 BC2 = AD × AC CD × AC
AB2 BC2 = AC (AD CD)
Since, AD CD = AC
Therefore, AC2 = AB2 BC2
Hence, the Pythagorean theorem is proved.
APPLICATIONS OF PYTHAGOREAN THEOREM
पाइथागोरस प्रमेय के कुछ अनुप्रयोग
- यह जानने के लिए कि त्रिभुज एक समकोण त्रिभुज है या नहीं
- एक वर्ग के विकर्ण को खोजने के लिए
- समकोण त्रिभुज में, हम किसी भी पक्ष की लंबाई की गणना कर सकते हैं यदि हम अन्य दो पक्षों की लंबाई जानते हैं
Source Page https://hindi.bankersadda.com/2020/04/pythagoras-theorem-definition-formula-and-examples.html
- answered 4 years ago
- Sandy Hook




Your Answer